Senaste nyheterna
Miniräknartips och trix del 1
2011-10-19Är du inget matematiskt snille? Har du ofta när du använd miniräknare funderat över vad vissa av knapparna betyder? Då har du en liten hjälp på traven här!
Trigonometriska funktioner byggger på vinklar, därav namnet som innbebär "Läran om förhållandet mellan vinklar och sidor i en triangel". Vissa av dessa förhållanden är så vanliga att de fått egna namn.
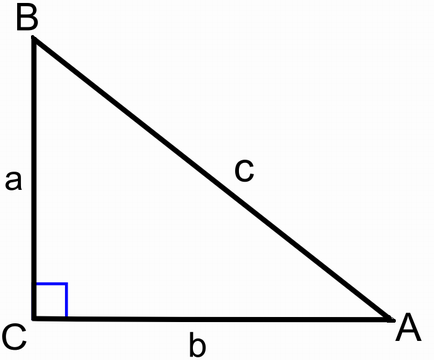
I en rätvinklig triangel som den på bilden ovan. Definieras så sin(A) (utläses: "Sinus för vinkeln A" eller kortare "sin-A") som förhållandet (kvoten) mellan längderna av sidan a och c. På samma förhåller sig cos(A)till sidorna b och c, samt tan(A) till sidorna a och b. Om du då vet åtminstone två vinklar och en sida i en triangel, kan du från förhållandena ovan bestämma de övriga sidorna och vinklarna!
Vad innebär då Arcsin, Arccos och Arctan? Enkelt uttryckt är det motsatsen till sin, cos respektive tan. Det vill säga, sin(45) (45 innebär här 45graders vinkel) ger dig svaret 1/sqrt(2) vilket är ungefär 0.707 så kommer Arcsin(1/sqrt(2)) ge dig svaret 45 grader! Alltså, Arcsin gör ogjort det sin har gjort. Arcsin(sin(A)) ger därför svaret A! Om du leker litegranna kommer du dock inse att du ibland får error. Detta beror på att Arcsin bara är definierade för värden mellan -90 och 90 grader på parametern. På samma sätt är Arccos bara definierat för värden mellan 0 och 180 grader. Arctan däremot fungerar för alla tänkbara värden på inparametern.
Vad har man då detta till? I vardagsmatte kan detta tyckas ganska onödigt, och ja det kanske det är. Men i till exempel mekanik, arkitektur och andra ämnen där man intresserar sig för sakers hållbarhet är tillämpningarna många!
