Simultaneous equations

Here we are going to show you how to solve simultaneous equations. Simultaneous equations are a set of equations containing multiple variables. We will show you a graphic solution, the substitute method and the addition method. We are not going to show you how to solve simultaneous equations using a matrix. That might be a later post.

Study these equations:

y = x + 8
y = 4x

There could be many solutions.

We want to find a value on X and Y that satisfies both equations.

Graphic solution

y= x + 5
y= 1,5x

If we draw both the lines on a paper it will look like this.

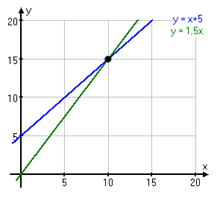
The point where the lines intersect has coordinates x=10 and y=15 and that is our solution. Simple as pie.

Sometimes we want a more exact solution and we don't want to draw any images. That's when you use an algebraic solution.

The substitute method

The idea in this method is that we substitute a variable in one equation with the corresponding expression in the other equation. We explain this with an example.

Study these equations:

2x - y = 7 
x = 3y + 1

If we are solving the first equation for Y (Put it alone on one side). We will get:

2x - y = 7 => y = 2x - 7

If we substitute y in the second equation with this expression (2x-7) we will get:

x = 3(2x - 7) + 1 => x = 6x - 21 + 1 => -5x = -20 => x = 4 

We now know x but we still want to find Y. We put the value for X in the first equation.

y=2x - 7 => y=2 * 4 - 7 => y= 8 * 7 => y=1

Answer: X=4 and Y=1 satisfies both equations.

The addition method

The idea here is to add the equations together. First we have to make sure that the coefficients in front of the Xes (or the Ys) adds to zero. Then you add the left side of the first equation with the left side of the second equation and the right side of the first equation with the right side of the second equation. The result is one equation with one variable. To make sure the coefficients adds to zero you may multiply one or both equations with a scalar.

Study these equations:

2x + y = 4
3x – y = 6

Since the coefficients in front of the Ys is +y and -y they add up zero already, we do not have to do any multiplication here. We ad both sides with each other and we get:

2x + y + 3x -y = 4 + 6 => 5x = 10 => x = 2

To get Y we just substitute Y to 2 in one equation:

2x + y = 4 => 2*2 + y = 4 => 4 + y = 4 => y=0

Answer: x=2 and y=0 satisfies both equations.

---

We can study an other example. Little more advanced this time.

Study these equations:

2x + y = 5
3x + 2y = 8

We can't add the equation together at once as we did in the previous example. We have to do some multiplication before. We see that if we multiply the first equation with 3 and the second equation with -2 then will the Xes add up to zero. Why we choose X here instead of Y does not really matter. You can choose the variable you think is easier.

2x + y = 5  =>  6x + 3y = 15
3x + 2y = 8 => -6x + -4y = -16

If we add the equations together:

6x + 3y - 6x + -4y = 15 – 16 => -y = -1 => y=1

To get X we just substitute Y to 1 in one equation:

2x + y = 5 => 2x + 1 = 5 => 2x = 4 => x=2

Answer: x=2 and y=1 satisfies both equations.